Introduction¶
Overview¶
The Pole EXpansion and Selected Inversion (PEXSI) method is a fast method for electronic structure calculation based on Kohn-Sham density functional theory. It efficiently evaluates certain selected elements of matrix functions, e.g., the Fermi-Dirac function of the KS Hamiltonian, which yields a density matrix. It can be used as an alternative to diagonalization methods for obtaining the density, energy and forces in electronic structure calculations. The PEXSI library is written in C++, and uses message passing interface (MPI) to parallelize the computation on distributed memory computing systems and achieve scalability on more than 10,000 processors.
From numerical linear algebra perspective, the PEXSI library can be used as a general tool for evaluating certain selected elements of a matrix function, and therefore has application beyond electronic structure calculation as well.
Given a sparse Hermitian matrix \(A\) and a certain function \(f(\cdot)\), the basic idea of PEXSI is to expand \(f(A)\) using a small number of rational functions (pole expansion)
and to efficiently evaluate \(f(A)_{i,j}\) by evaluating selected elements \((A-z_l I)^{-1}_{i,j}\) (selected inversion).
The currently supported form of \(f(\cdot)\) include:
- \(f(z)=z^{-1}\): Matrix inversion. Since the matrix inversion is already represented as a single term of rational function (pole), no pole expansion is needed. The selected inversion method can be significantly faster than directly inverting the matrix and then extract the selected elements of the inverse. For only using PEXSI to evaluate selected elements of \(A^{-1}\), see Selected Inversion of complex for an example.
- \(f(z)=\frac{2}{1+e^{\beta (z-\mu)}}\): Fermi-Dirac function. This can be used as a “smeared” matrix sign function at \(z=\mu\), without assuming a spectral gap near \(z=\mu\). This can be used for evaluating the electron density for electronic structure calculation. See Solving Kohn-Sham DFT: I for an example using PEXSI for electronic structure calculation.
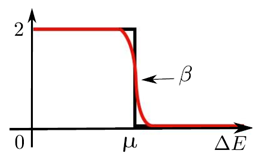
Red: Fermi-Dirac function. Black: Matrix sign function
For sparse matrices, the PEXSI method can be more efficient than the widely used Diagonalization method for evaluating matrix functions, especially when a relatively large number of eigenpairs are needed to be computed in the diagonalization method. PEXSI can also be used to compute the matrix functions associated with generalized eigenvalue problems, i.e.
where \(V,\Lambda\) are defined through the generalized eigenvalue problem \(A V = B V \Lambda\).
PEXSI is most advantageous when a large number of processors are available, due to the two-level parallelism. It is most advantageous to use PEXSI when at least 1000 cores are available, and for many problems PEXSI can scale to tens of thousands of cores.
For details of the implementation of parallel selected inversion used in PEXSI, please see TOMS2016 below.
Diagonalization method
- The diagonalization method evaluates a matrix function \(f(A)\) by \(f(A) = V f(\Lambda) V^{-1}\), where the orthonormal matrix \(V=[v_1,\ldots,v_N]\), and the diagonal matrix \(\Lambda=\mathrm{diag}(\lambda_1,\ldots,\lambda_N)\) are defined through the eigenvalue problem \(A V = V \Lambda\) It is often the case that not all eigenvalues \({\lambda_i}\) are needed to be computed, depending on the value of \(f(\lambda_i)\).
Selected elements
- For (real or complex) symmetric matrices (i.e. \(A_{i,j}\ne 0\) implies \(A_{j,i}\ne 0\)), we define the selected elements of a matrix \(B\) with respect to a matrix \(A\) as the set \(\{B_{i,j}\vert A_{i,j}\ne 0\}\).
- A commonly used case in PEXSI is the selected elements of \(A^{-1}\) with respect to a (real or complex) symmetric matrix \(A\), or simply the selected elements of \(A^{-1}\), which corresponds to the set \(\{A^{-1}_{i,j} \vert A_{i,j}\ne 0\}\).
- For general non-symmetric matrices, the selected elements are \(\{B_{i,j}\vert A_{j,i}\ne 0\}\). NOTE: this means that the matrix elements computed corresponding to the sparsity pattern of \(A^T\) (for more detailed explanation of the mathematical reason, please see the paper PC2018 below). However, storing the matrix elements \(\{A^{-1}_{i,j}\vert A_{j,i}\ne 0\}\) is practically cumbersome, especially in the context of distributed computing. Hence we choose to store the selected elements for \(A^{-T}\), i.e. \(\{A^{-T}_{i,j}\vert A_{i,j}\ne 0\}\). These are the values obtained from the non-symmetric version of PSelInv.
- One particular problem arising from electronic structure theory is when the Hamiltonian matrix and the overlap matrix \(H,S\) are Hermitian matrices, and the matrix to be inverted are of the form \((H-zS)^{-1}\). This matrix is only structurally symmetric, and we need to call the non-symmetric version of PSelInv. From the discussion above, the computed matrix entries are actually \(\{(H-zS)^{-T}_{i,j}\vert A_{i,j}\ne 0\}\). Combining with the pole expansion, we obtain \(P^T\), which is the transpose of the density matrix. Since the density matrix Hermitian, we have \(P=P^*=\overline{P^T}\). Hence we perform an extra conjugation as a post-processing step to obtain the correct density matrix.
PEXSI used in external packages¶
Please let us know if PEXSI is useful for your application or software package!
BigDFT
CP2K
- Tutorials for compiling CP2K-PEXSI: http://www.cp2k.org/howto:compile
DFTB+
ESL Bundle
FHI-aims
Quantumwise ATK
SIESTA
- Download link for SIESTA-PEXSI: https://launchpad.net/siesta
Electronic Structure Infrastructure (ELSI) Project
- http://www.elsi-interchange.org/webpage/
- In the future, the support of PEXSI for electronic structure software packages will be provided mainly through the ELSI project.
License¶
PEXSI is distributed under BSD license (modified by Lawrence Berkeley National Laboratory).
PEXSI Copyright (c) 2012 The Regents of the University of California, through Lawrence Berkeley National Laboratory (subject to receipt of any required approvals from U.S. Dept. of Energy). All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
(1) Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer. (2) Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution. (3) Neither the name of the University of California, Lawrence Berkeley National Laboratory, U.S. Dept. of Energy nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS “AS IS” AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
You are under no obligation whatsoever to provide any bug fixes, patches, or upgrades to the features, functionality or performance of the source code (“Enhancements”) to anyone; however, if you choose to make your Enhancements available either publicly, or directly to Lawrence Berkeley National Laboratory, without imposing a separate written license agreement for such Enhancements, then you hereby grant the following license: a non-exclusive, royalty-free perpetual license to install, use, modify, prepare derivative works, incorporate into other computer software, distribute, and sublicense such enhancements or derivative works thereof, in binary and source code form.
Contributors¶
- Lin Lin, UC Berkeley and Lawrence Berkeley National Laboratory, linlin@math.berkeley.edu
- Weinan E, Princeton University, weinan@math.princeton.edu
- Mathias Jacquelin, Lawrence Berkeley National Laboratory, mjacquelin@lbl.gov
- Weile Jia, UC Berkeley, wjia@lbl.gov
- Jianfeng Lu, Duke University, jianfeng@math.duke.edu
- David Williams-Young, David Williams-Young, dbwy@lbl.gov,
- Chao Yang, Lawrence Berkeley National Laboratory, cyang@lbl.gov
- Lexing Ying, Stanford University, lexing@stanford.edu
- Victor Yu, Duke University, wenzhe.yu@duke.edu
Citing PEXSI¶
If you use PEXSI for electronic structure calculation in general, please cite the following two papers.:
@Article{CMS2009,
Title = {Fast algorithm for extracting the diagonal of the inverse matrix with application to the electronic structure analysis of metallic systems},
Author = {Lin, L. and Lu, J. and Ying, L. and Car, R. and E, W.},
Journal = {Comm. Math. Sci.},
Year = {2009},
Pages = {755},
Volume = {7}
}
@Article{JCPM2013,
Title = {Accelerating atomic orbital-based electronic structure calculation via pole expansion and selected inversion},
Author = {Lin, L. and Chen, M. and Yang, C. and He, L.},
Journal = {J. Phys. Condens. Matter},
Year = {2013},
Pages = {295501},
Volume = {25}
}
If you use PEXSI for selected inversion (PSelInv), please also cite the following paper.:
@Article{TOMS2016,
Title = {{PSelInv}--A distributed memory parallel algorithm for selected inversion: the symmetric case},
Author = {Jacquelin, M. and Lin, L. and Yang, C.},
Journal = {ACM Trans. Math. Software},
Year = {2016},
Pages = {21},
Volume = {43}
}
If you use the non-symmetric version of PSelInv, please also cite the following paper.:
@Article{PC2018,
Title = {{PSelInv}--A distributed memory parallel algorithm for selected inversion: the non-symmetric case},
Author = {Jacquelin, M. and Lin, L. and Yang, C.},
Journal = {Parallel Comput.},
Year = {2018},
Pages = {74},
Volume = {84}
}
More references on method development:
M. Jacquelin, L. Lin and C. Yang, PSelInv ? A distributed memory parallel algorithm for selected inversion: the non-symmetric case, Parallel Comput. 74, 84, 2018 link.
M. Jacquelin, L. Lin, W. Jia, Y. Zhao and C. Yang, A left-looking selected inversion algorithm and task parallelism on shared memory systems, HPC Asia, 54, 2018
V. Wen-zhe Yu, F. Corsetti, A. Garcia, W. Huhn, M. Jacquelin, W. Jia, B. Lange, L. Lin, J. Lu, W. Mi, A. Seifitokaldani, A. Vazquez-Mayagoitia, C. Yang, H. Yang and V. Blum, ELSI: A Unified Software Interface for Kohn-Sham Electronic Structure Solvers, Commun. Phys. Comput. 222, 267, 2018 link.
W. Jia and L. Lin, Robust Determination of the Chemical Potential in the Pole Expansion and Selected Inversion Method for Solving Kohn-Sham density functional theory, J. Chem. Phys. 147, 144107, 2017 link.
M. Jacquelin, L. Lin, N. Wichmann and C. Yang, Enhancing the scalability and load balancing of the parallel selected inversion algorithm via tree-based asynchronous communication, IEEE IPDPS, 192, 2016 link.
M. Jacquelin, L. Lin and C. Yang, PSelInv ? A distributed memory parallel algorithm for selected inversion : the symmetric case, ACM Trans. Math. Software 43, 21, 2016 link.
L. Lin, A. Garcia, G. Huhs and C. Yang, SIESTA-PEXSI: Massively parallel method for efficient and accurate ab initio materials simulation without matrix diagonalization, J. Phys. Condens. Matter 26, 305503, 2014 link.
L. Lin, M. Chen, C. Yang and L. He, Accelerating atomic orbital-based electronic structure calculation via pole expansion and elected inversion, J. Phys. Condens. Matter 25, 295501, 2013 link.
L. Lin, C. Yang, J. Meza, J. Lu, L. Ying and W. E, SelInv – An algorithm for selected inversion of a sparse symmetric matrix, ACM Trans. Math. Software 37, 40, 2011 link.
L. Lin, C. Yang, J. Lu, L. Ying and W. E, A Fast Parallel algorithm for selected inversion of structured sparse matrices with application to 2D electronic structure calculations, SIAM J. Sci. Comput. 33, 1329, 2011 link.
L. Lin, J. Lu, L. Ying, R. Car and W. E, Fast algorithm for extracting the diagonal of the inverse matrix with application to the electronic structure analysis of metallic systems, Commun. Math. Sci. 7, 755, 2009 link.
L. Lin, J. Lu, L. Ying and W. E, Pole-based approximation of the Fermi-Dirac function, Chin. Ann. Math. 30B, 729, 2009 link.
Some references on applications of PEXSI
W. Hu, L. Lin, C. Yang, J. Dai and J. Yang, Edge-modified phosphorene nanoflake heterojunctions as highly efficient solar cells, Nano Lett. 16 1675, 2016
W. Hu, L. Lin and C. Yang, DGDFT: A massively parallel method for large scale density functional theory calculations, J. Chem. Phys. 143, 124110, 2015
W. Hu, L. Lin and C. Yang, Edge reconstruction in armchair phosphorene nanoribbons revealed by discontinuous Galerkin density functional theory, Phys. Chem. Chem. Phys. 17, 31397, 2015
W. Hu, L. Lin, C. Yang and J. Yang, Electronic structure of large-scale graphene nanoflakes, J. Chem. Phys. 141, 214704, 2014
Developer’s documentation¶
This document is generated with Sphinx. For more detailed API routines in C/C++/FORTRAN see the developer’s documentation generated by doxygen. To obtain this document, type doxygen under the pexsi directory, and the document will appear in the developerdoc directory.
PEXSI version history¶
v2.0.0 (2/27/2022)
- New cmake system (require CMake version 3.17+) simplifying the installation process.
- New poles based on minimax optimization procedure (method 2), and update the adaptive Antoulas-Anderson (AAA) method (method 3). Both methods can now support the calculation of the free energy density matrix and energy density matrix without the additional inverse of the S matrix.
- Compatible with SuperLU_DIST 7.2.0 (Note: SuperLU_DIST 7.2.0 introduces breaking changes. Previous versions of SuperLU_DIST will not be supported)
- Add “method 3” in the pole expansion, which uses the adaptive Antoulas-Anderson (AAA) method for pole expansion. This is now the default pole expansion method. The AAA method uses similar number of poles as “method 2” (Moussa’s optimization procedure) for the Fermi-Dirac function, and supports the evaluation of free energy density matrix and energy density matrix as well
- Bug fix: EDMCorrection with method 2 when H,S are complex Hermitian (contributed by Victor Yu).
- Reorganize the code for performing EDMCorrection, and the code for the perhaps confusing transpose operations needed for computing the density matrix, energy density matrix and free energy density matrix, when H,S are complex Hermitian.
- v1.2.0 (1/8/2019)
- PEXSI documentation migrate to https://pexsi.readthedocs.io
- PEXSI open source code available at https://bitbucket.org/berkeleylab/pexsi
- Introduce CMake compilation (require CMake version 3.10+). Updated documentation related to cmake (this is the prefered way for compiling PEXSI in the future)
- Compatible with SuperLU_DIST 6.1.0 (Note: SuperLU_DIST 6.0+ introduces breaking changes. Previous versions of SuperLU_DIST will not be supported)
- v1.0.3 (7/20/2018)
- Bug fix: consistency problem in the data type of fortran examples (contributed by Calvin Anderson).
v1.0.2 (7/17/2018)
- Bug fix: When H and S are Hermitian matrices, return the proper density matrix and energy density matrix from CalculateFermiOperatorComplex, instead of its transpose. This is done by transposing the e.g. density matrix due to the Hermitian property. (contributed by Victor Yu)
- Clarify the documentation for the treatment of selected elements of non-symmetric matrices.
- Fix the naming of SRealMat and SComplexMat in ppexsi.cpp.
- v1.0.1 (6/20/2018)
- Bug fix: initialization error in driver_fermi_complex, and uninitialized variables in CalculateFermiOperatorComplex
- v1.0 (10/22/2017)
Introduce PPEXSIDFTDriver2. This reduces the number of user-defined parameters, and improves the robustness over PPEXSIDFTDriver.
Compatible with the ELSI software package.
Migrate from doxygen to sphinx for documentation. The original doxygen format is still kept for the purpose of developers.
symPACK replaces SuperLU_DIST as the default solver for factorizing symmetric matrices. SuperLU_DIST is still the default solver for factorizing unsymmetric matrices. Currently supported version of SuperLU_DIST is v5.1.3.
PT-Scotch replaces ParMETIS as the default matrix ordering package. ParMETIS is still supported. Currently supported version of PT-Scotch is v6.0
Support Moussa’s optimization based pole expansion.
Moussa, J., Minimax rational approximation of the Fermi-Dirac distribution, J. Chem. Phys. 145, 164108 (2016)
Pole expansion given by src/getPole.cpp generated by a utility file. This allows types of pole expansions other than discretization of the contour integral to be implemented in the same fashion.
Compatible with spin-polarized and k-point parallelized calculations.
- v0.10.1 (11/8/2016)
- Bug fix: matrix pattern for nonzero overlap matrices and missing option in fortran interface (contributed by Victor Yu)
v0.10.0 (11/6/2016)
- Combine LoadRealSymmetricMatrix / LoadRealUnsymmetricMatrix into one single function LoadRealMatrix. Similar change for LoadComplexMatrix. The driver routines and output are updated as well.
- Updated makefile (contributed by Patrick Seewald)
- Compatible with SuperLU_DIST_v5.1.2
- Replace the debugging with PushCallStack / PopCallStack debugging by Google’s coredumper.
- A number of new example driver rouintes in examples/ and fortran/
- Experimental feature: Add CalculateFermiOperatorComplex function. The implementation corresponds to CalculateFermiOperatorReal, but is applicable to the case when H and S are complex Hermitian matrices. This feature will facilitates the future integration with the Electronic Structure Infrastructure (ELSI) project.
- Experimental feature: integration with symPACK for LDLT factorization.
- Bug fix: Initialization variable pstat in interface with SuperLU_DIST
- Bug fix: Add (void*) in MPI_Allgather of sparseA.nnzLocal in utility_impl.hpp.
- v0.9.2 (2/29/2016)
- Add support for SuperLU_DIST v4.3. Starting from v0.9.2, the SuperLU_DIST v3.3 version is NO LONGER SUPPORTED.
- Change the compile / installation to the more standard make / make install commands.
- Add pole expansion C/FORTRAN interfaces that can be called separately.
- Bug fix: remove a const attribute in CSCToCSR since it is modified by MPI. Add (void*) to MPI_Allgather for some compilers.
- Bug fix: Mathjax is upgraded to v2.6 to support chrome rendering.
- Add DFTDriver2 which allows only one PEXSI iteration per SCF iteration. This requires a careful setup of the inertia counting procedure.
- In DFTDriver2, the muMinInertia and muMaxInertia are updated to avoid the true chemical potential to be at the edge of an interval.
- v0.9.0 (07/15/2015)
- Add parallel selected inversion (PSelInv) for asymmetric matrices. The asymmetric matrix can be either structurally symmetric or fully asymmetric.
- Add the example routines and fortran interfaces for asymmetric selected inversion.
- Simplify the interface for installation.
- (Contributed by Patrick Seewald) Bug fix: output string for SharedWrite utility routine.
- v0.8.0 (05/11/2015)
Improve the data communication pattern for PSelInv. The parallel scalability of PSelInv is much improved when more than 1000 processors are used. The variation of running time among different instances is also reduced.
For more details of the improvement see
M. Jacquelin, L. Lin, N. Wichmann and C. Yang, Enhancing the scalability and load balancing of the parallel selected inversion algorithm via tree-based asynchronous communication, submitted [<a href=”http://arxiv.org/abs/1504.04714”>arXiv</a>]
Templated implementation of a number of classes including SuperLUMatrix.
Update the structure of the include/ folder to avoid conflict when PEXSI is included in other software packages.
Update the configuration files. Remove the out-of-date profile options.
Bug fix: MPI communicator in f_driver_ksdft.f90.
v0.7.3 (11/27/2014) - Multiple patches suggested by Alberto Garcia.
- Fix a bug in the “lateral expansion” for locating the bracket for the chemical potential.
- Search for band edges of the chemical potential, which serve both for metals and for systems with a gap.
- Add a paramter (mu0 in in PPEXSIOptions) to provide the starting guess of chemical potential. This can be used for the case in which the PEXSI solver is invoked directly, without an inertia-counting phase.
- Update the example drivers accordingly to these bug fixes.
v0.7.2 (08/27/2014) - Bug fix: Two temporary variables were not initialized during the computation of the number of electrons and its derivatives. - Add test matrices to the fortran/ folder as well. - Update the configuration files.
v0.7.1 (07/01/2014) - Bug fix: PPEXSIPlanInitialize specifics the input according to mpirank instead of outputFileIndex. - Bug fix: PPEXSIPlanFinalize gives floating point error due to the double deallocation of SuperLUGrid.
v0.7.0 (05/24/2014) - Use PPEXSIPlan to coordinate the computation, and allows the code to be used for C/C++/FORTRAN. - Templated implementation and support for both real and complex arithmetic. - New interface routines for FORTRAN based on ISO_C_BINDING (FORTRAN 2003 and later). - Basic interface for KSDFT calculation, with a small number of input parameters and built-in heuristic strategies. - Expert interface for KSDFT calculation, providing full-control of the heuristics. - Symbolic factorization can be reused for multiple calculations. - Enhanced error estimate for the pole expansion using energy as a guidance.
v0.6.0 (03/11/2014) - Version integrated with the SIESTA package for Kohn-Sham density functional theory (KSDFT) calculation. - Parallel selected inversion for complex symmetric matrices. - Estimate the density of state profile via inertia counting. - Compute the density of states and local density of states.